矩阵图法

矩阵图法简介
　　矩阵图法就是从多维问题的事件中，找出成对的因素，排列成矩阵图，然后根据矩阵图来分析问题，确定关键点的方法，它是一种通过多因素综合思考，探索问题的好方法。
　　在复杂的质量问题中，往往存在许多成对的质量因素，将这些成对因素找出来，分别排列成行和列，其交点就是其相互关联的程度，在此基础上再找出存在的问题及问题的形态，从而找到解决问题的思路。
　　矩阵图的形式如下图所示，A为某一个因素群，a1、a2、a3、a4、…是属于A这个因素群的具体因素，将它们排列成行；B为另一个因素群，b1、 b2、b3、b4、…为属于B这个因素群的具体因素，将它们排列成列；行和列的交点表示A和B各因素之间的关系，按照交点上行和列因素是否相关联及其关联程度的大小，可以探索问题的所在和问题的形态，也可以从中得到解决问题的启示等。
ngdesc="/wiki/Image:%E7%9F%A9%E9%98%B5%E5%9B%BE%E7%A4%BA%E6%84%8F%E5%9B%BE.gif" />
　　质量管理中所使用的矩阵图，其成对因素往往是要着重分析的质量问题的两个侧面，如生产过程中出现了不合格时，着重需要分析不合格的现象和不合格的原因之间的关系，为此，需要把所有缺陷形式和造成这些缺陷的原因都罗列出来，逐一分析具体现象与具体原因之间的关系，这些具体现象和具体原因分别构成矩阵图中的行元素和列元素。
　　矩阵图的最大优点在于，寻找对应元素的交点很方便，而且不会遗漏，显示对应元素的关系也很清楚。矩阵图法还具有以下几个特点：
　　①可用于分析成对的影响因素；
　　②因素之间的关系清晰朋了，便于确定重点；
　　③便于与系统图结合使用。
矩阵图法的用途
　　矩阵图法的用途十分广泛，在质量管理中，常用矩阵图法解决以下问题：
　　①把系列产品的硬件功能和软件功能相对应，并要从中找出研制新产品或改进老产品的切入点；
　　②明确应保证的产品质量特性及其与管理机构或保证部门的关系，使质量保证体制更可靠；
　　③明确产品的质量特性与试验测定项目、试验测定仪器之间的关系，力求强化质量评价体制或使之提高效率；
　　④当生产工序中存在多种不良现象，且它们具有若干个共同的原因时，希望搞清这些不良现象及其产生原因的相互关系，进而把这些不良现象一举消除；
　　⑤在进行多变量分析、研究从何处入手以及以什么方式收集数据。
矩阵图的类型
　　矩阵图法在应用上的一个重要特征，就是把应该分析的对象表示在适当的矩阵图上。因此，可以把若干种矩阵图进行分类，表示出他们的形状，按对象选择并灵活运用适当的矩阵图形。常见的矩阵图有以下几种：
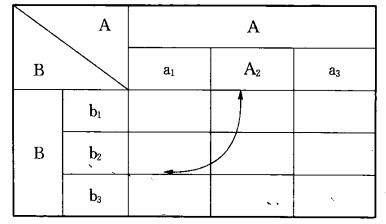
　　(1)L型矩阵图。L形矩阵图是最基本的矩阵图，是最为常见，且使用较多者。用来表示两组事件之间的关系，或关系的程度，也适用于各种结果与原因的关系。
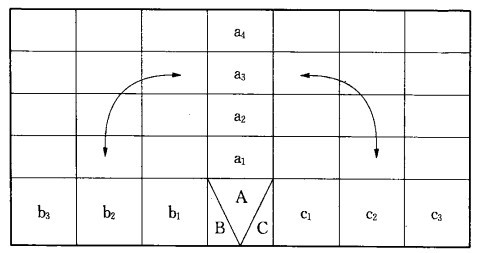
ngdesc="/wiki/Image:L%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　(2)T型矩阵图。T形矩阵图是用来表示A、B两组事件及A、C两组事件，两两之间的关系。亦即，将A与B的L形矩阵图，和B与C的L形矩阵图连接，以B共通而组合成T字形的矩阵图，由图中可看出B与A、C间的关系。
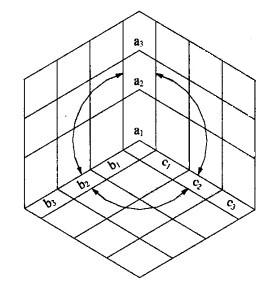
ngdesc="/wiki/Image:T%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　(3)Y型矩阵图。Y形矩阵图是由A与B、B与C、A与C的三个L形矩阵图所组合而成的矩阵图，因其外形类似Y字，所以称为Y形矩阵图。可以清楚表达出：①A与B、C，②B与A、C，③C与A、B，彼此间的关系。
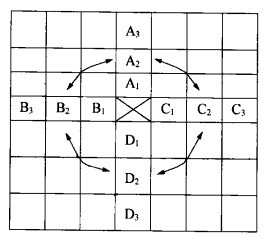
ngdesc="/wiki/Image:Y%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　(4)X型矩阵图。X形矩阵图是由A与B、B与C、C与D、D与A的四个L形矩阵图所组合而成，因其外形类似X字，所以称为X形矩阵图。可以清楚表达出：①A与B、D，②B与A、C，③C与B、D，④D与A、C，彼此间的关系。
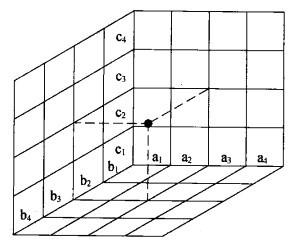
ngdesc="/wiki/Image:X%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　(5)C型矩阵图。C形矩阵图最复杂，用来表示A、B、C三组事件的立体空间上的关系。其特点是以A、B、C各因素在三度空间上的交点为构想点
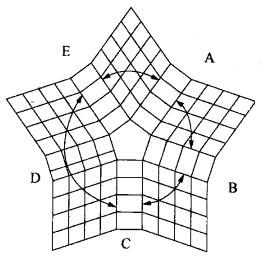
ngdesc="/wiki/Image:C%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　(6)P型矩阵图
ngdesc="/wiki/Image:P%E5%9E%8B%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
制作矩阵图的步骤
　　制作矩阵图一般要遵循以下几个步骤：
　　①列出质量因素；
　　②把成对因素排列成行和列，表示其对应关系；
　　③选择合适的矩阵图类型；
　　④在成对因素交点处表示其关系程度，一般凭经验进行定性判断，可分为三种：关系密切、关系较密切、关系一般(或可能有关系)，并用不同符号表示；
　　⑤根据关系程度确定必须控制的重点因素；
　　⑥针对重点因素作对策表。
矩阵图法的应用举例
　　实例一：
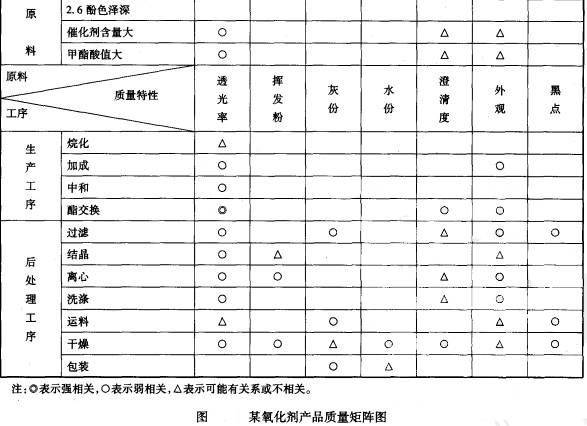
　　某厂为提高产品的性能，从各工序和原料人手，分析查找原因，通过做T型矩阵图(如下图)，对影响质量的工序和原材料进行分析筛选，找出了影响质量的主要工序和原料，并采取了有效措施，提高了质量。
ngdesc="/wiki/Image:%E6%9F%90%E6%B0%A7%E5%8C%96%E5%89%82%E4%BA%A7%E5%93%81%E8%B4%A8%E9%87%8F%E7%9F%A9%E9%98%B5%E5%9B%BE.jpg" />
　　实例二：
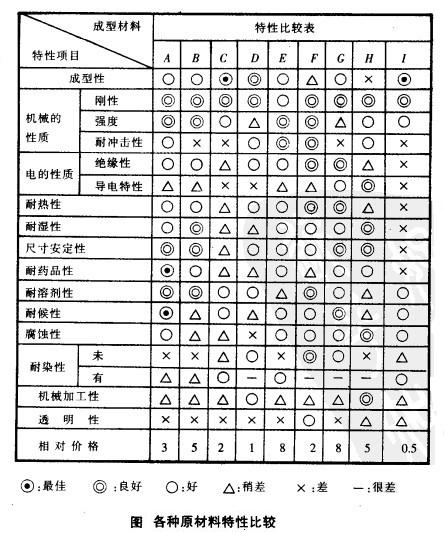
　　某成型加工厂的制品特性为应顾客要求的，需经常改变，因而常为要选择适合的原料而倍感困扰，有时甚至因选到不适用的原材料而使制品成为废品，造成重大的损失。该公司于是由有关人员组成小组，收集各种有关标准，并利用公司过去的有关原材料特性与制品特性之相关性数据，借着矩阵图法将之加以整理如下图，作为日后原材料选择的依据。(L形矩阵图)
ngdesc="/wiki/Image:%E5%90%84%E7%A7%8D%E5%8E%9F%E6%9D%90%E6%96%99%E7%89%B9%E6%80%A7%E6%AF%94%E8%BE%83.jpg" />
相关链接 QC旧七大手法：管制图、直方图、散布图、因果图、柏拉图、检查表、层别法。QC新七大手法：矩阵图法、KJ法、关系图法、系统图法、矩阵数据分析法、PDPC法、箭形图解法。